Решите уравнение: 1/х(х-2) + 2/(х-1)^2 =2
Другие вопросы по теме Алгебра
Популярные вопросы
- 111- бет4-тапсырма мәтінге 5 сөйлемге түрлі нұсқада сұрақ қой....
2 - Очень второй и четвёртый вариант...
1 - Решите рівняння 4 1/8-2 7/12= 2 5/6...
3 - 2. Обчисліть висоту вершини, якщо відомо, що на рівні моря атмосферний...
3 - У чому білгородське возного тетерваковського на початку твору...
3 - План сочинения по литературе Дубровский ...
3 - Описание быта и нравов купеческой семьи из Песня про царя Ивана Васильевича...
1 - Найти ускорение свободного падения...
2 - ОЧЕНЬ Укажіть речення з простими дієслівними присудками: А. Я хочу погостювати...
2 - Выписать из романа «Отцы и дети» 10 предложений с приложением. Обосновать,...
1
ОДЗ: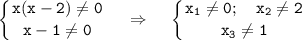
Пусть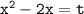 , получим
, получим 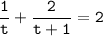
Умножим левую и правую части уравнения на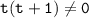 , получим
, получим
Возвращаемся к обратной замене