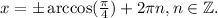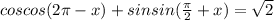 решите тригонометрическое уравнение
решите тригонометрическое уравнение
Другие вопросы по теме Алгебра
Популярные вопросы
- 1406. який відрізок довший: той, у якого 0,2 від половини довжини дорівнює...
3 - 1) территории которые вошли в состав после победы в вов. 2) судьба германии...
1 - Sin ^2x + 2 cos^2x -5 cos x - 7 = 0...
3 - Уточните, что понимается под духовностью и соборностью, когда речь идет...
3 - Проверочные слова к словам соками,что-нибудь.первое слово если кто нибудь...
2 - Уменьшите число 18: а) в 3 раза; б) на 3; в)в 9 раз; г)на 9...
1 - Отредактировать текст в некотором царстве в некотором государстве жил колобок....
2 - Мальчик на 3000 р . купил блокнот , ручку , карандаш и резинку . ручка...
3 - Сколько звуков [о] в отрывке из стихотворения: тренькает синица меж лесных...
3 - какие художественные средства есть в сказке репка и назовите их!...
1
ОТВЕТ: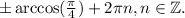
Используем формулы приведения:
Разделим обе части на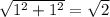 :
:
Разберемся с правой частью. На множестве действительных чисел косинус принимает значения от -1 до 1 включительно, поэтому выражение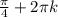 должно попадать в данный промежуток значений. С учётом того, что
должно попадать в данный промежуток значений. С учётом того, что 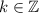 , это возможно только при
, это возможно только при 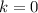
(формально решаем неравенство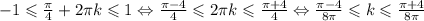 , имеющее единственное целое решение - число 0, поскольку левая часть > -1, а правое < 1)
, имеющее единственное целое решение - число 0, поскольку левая часть > -1, а правое < 1)
т.е. окончательно получаем, что
Отсюда