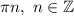Решите тригонометрическое уравнение
Другие вопросы по теме Алгебра
Популярные вопросы
- Запишіть слова кожної групи за алфавітом. 1. арка, дрова, посуд, трагедія,...
3 - Как пишится работа на башкирском языке...
1 - Выписать слова с безударными гласными в корне и слова с согласными звуками,...
1 - Перевод ! 5 класс книга спортлайт 1 как выглядит твоя новая квартира? на...
1 - Використали на 1костюм 4 м використали тканини 36 м кількість костюмов?...
2 - Надо) напишите уравнение реакции с которых можно осуществить следующие...
2 - Охарактеризувати козака швайку дуже потібно пліз...
1 - Как переводится can i have some more cake , please ? where s your mum ,...
1 - 46030 дм2 надо перевести в квадратные метры и дециметры...
1 - Куда макар телят не гонял составить предложения...
2
Уравнение распадается на совокупность двух уравнений:
Решаем первое уравнение:
Применяем формулу косинуса двойного угла:
Решаем второе уравнение:
Последнее уравнение не имеет корней.
ответ: