Решите системы уравнений.
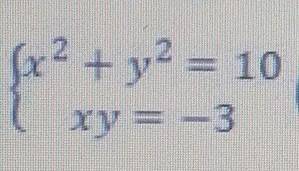
Другие вопросы по теме Алгебра
Популярные вопросы
- Написать 1 закличку и поговорку с ответами...
1 - Жатыс септік окончание к словам қас,қаңтар,үй,сабақ,жұмыс,нұрбол...
1 - 3. задайте вопросы к выделенным словам: 1. medicines are compounded, dispensed,...
3 - Бобчинский и добчинский как ведет себя чиновник , когда пытается дать взятку хлестакову(...
3 - Напишите мне 15) животных долгожителей. это...
1 - Садовод вырастил и продал 2000 цветов,роз 450. это в 2 раза меньше,чем астр, а...
2 - Что разбил мальчик из рассказа валентины осеевой почему?...
1 - Араб тілінен енген сөздердің нұсқасымен тауып беріндерші...
2 - Мы гуляли около двадцатого дома каким членом предложения является слово двадцатого...
1 - 1)17(-5x-1)-9(17x-3) 2)23b-4-7(4-19b)...
3
Решим систему методом подстановки.
Выпишем первое уравнение отдельно и решим его.
Решаем биквадратное уравнение:
Теперь найдем х:
ответ: (-1;3), (1;-3), (-3;1), (3;-1)