Решите систему уравнений: { x+xy+y=5 { y+yz+z=11 { z+zx+x=7 нужно подробное решение! 16 пунктов за решение!

Ответы

Nikita82279 23.05.2020 16:14

$\begin{cases} x+xy+y=5\\y+yz+z=11\\z+zx+x=7 \end{cases}$

Решение

Преобразуем, из первого уравнения выразим x

$\begin{cases} x*(1+y)+y=5\\y+yz+z=11\\z+zx+x=7 \end{cases}$

$\begin{cases} x=\frac{5-y}{1+y}\\y+yz+z=11\\z+zx+x=7 \end{cases}$

теперь это выражение поставим в третье уравнение, получим:

$\{ {{y+yz+z=11} \atop {z+z*(\frac{5-y}{1+y})+(\frac{5-y}{1+y})=7}} \$

Из первого уравнения выражаем z, получим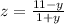 $z=\frac{11-y}{1+y}$

Это выражение подставим во второе уравнение получим с одной нейзвестной, преобразуем его найдем игрик:

$(\frac{11-y}{1+y})+(\frac{11-y}{1+y})*(\frac{5-y}{1+y})+(\frac{5-y}{1+y})=7$

$\frac{(11-y)*(1+y)^2+(11-y)*(5-y)*(1+y)}{(1+y)^3}+(\frac{5-y}{1+y})=7</p
<p$

Я вам не буду досканально раписывать, формулы километровые

Получим y1=-4, y2=2.

вычислим x1=5-(-4)/1+(-4)=-3; x2=5-2/1+2=1

вычислим z1=11-(-4)/1+(-4)=-5; z2=11-2/1+2=3

ответ: x1=-3 ; y1=-4; z1=-5;

x2=1; y2=2; z2=3.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

zatheeva 21.07.2019 07:20

neondragooffi 21.07.2019 07:20

36+74 делится на 5; 37+45 делится на 2?...

Себастиаан 21.07.2019 07:20

Выполните умножение: а) (y-3)(y+8) б) (x+4)(9+x) в) (3b-2a)(7a+5b)...

Daniyal11111111 21.07.2019 07:20

YULEMESLEILAA 21.07.2019 07:20

(x-2)(x+2)=2(x-1)^2-x^2 нужно решить...

yan4enkomaks 21.07.2019 07:20

kiskammp014dd 21.07.2019 07:20

малая555 21.07.2019 07:20

kazakov1206 21.07.2019 07:10

Решите уравнение б)4y^3-y=0 в)x^4-x^2=0 г)9y^2-4y^4=0...

bolatbekaliya 21.07.2019 07:10