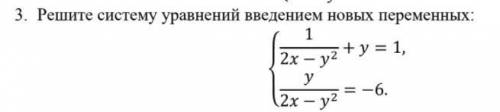
Решите систему уравнений введением новых переменных
Другие вопросы по теме Алгебра
Популярные вопросы
- Решить систему графическим методом. {4y+x=11; 5x-2y=17...
3 - Найди значение выражения при а=2...
3 - 1)Побудуйте трикутник АВС за сторонами і кутом АВ = 7 , ВС = 5 , що...
2 - Из ионов: OH- ; H+ ; Fe3+; NO3 - ; SO42- ;Mg2+, получи химическую формулу...
1 - - Скажите, что вы и ваши друзья обязательно сделают то, что собираются...
3 - КОД 10 12.0,ВПР. Биология. 7 класс. Вариант 21313.1. Рассмотрите изображения...
3 - В вопросах 1 и 3 ответ введите в виде десятичной дроби. В вопросах 2...
2 - Из неживой природы в живую вода, углекислый газ и минеральные соли поступают...
3 - Куш бiлекте емес, журекте «Батыр туса-ел ырысы» тақырыбындағы жазба...
2 - 3-тапсырма. Асқар Алтайдың «Прописка» әңгімесі Әңгімедегі кейіпкерлер...
3
Объяснение:
1) y₁=-2.
2) y₂=3.
ответ: (2¹/₆;-2), (4¹/₄;3).