1. Алгебра
  2. Решите систему уравнений Решите

Решите систему уравнений Решите систему уравнений

VTKOF VTKOF    1   30.05.2020 16:01    0

Ответы
artemafanasev2003 artemafanasev2003  15.10.2020 11:06

Рассмотрим второе уравнение и заметим, что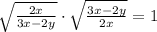 \sqrt{\frac{2x}{3x-2y} }\cdot\sqrt{\frac{3x-2y}{2x}}=1

Сделаем замену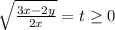 \sqrt{\frac{3x-2y}{2x}}=t\geq 0. В итоге имеем:

t+\frac{1}{t}=2,\\\\t^2-2t+1=0\Rightarrow t=1

Т.е.

\sqrt{\frac{3x-2y}{2x}}=1\Rightarrow\frac{3x-2y}{2x}=1,\\\\ 3x-2y=2x\Rightarrow x=2y

Подставляем в первое уравнение:

x^2-18=x(2x-9);\\\\x^2-18=2x^2-9x;\\\\x^2-9x+18=0.

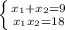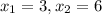По теореме Виета \left \{ {{x_1+x_2=9} \atop {x_1x_2=18}} \right., откуда x_1=3, x_2=6.

Из равенства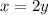 x=2y находим y:

y=\frac{x}{2};\\\\ y_1=\frac{x_1}{2}=\frac{3}{2},\\\\ y_2=\frac{x_2}{2}=\frac{6}{2}=3

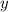ОТВЕТ: (3; 1,5), (6; 3).

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
LOxxx24124 LOxxx24124  21.05.2019 02:00
Решить уравнение: cosx+cos2x+cos6x+cos7x=0...
nadyamoroz03 nadyamoroz03  21.05.2019 02:00
Сократите дроби *заранее за решение* а) 14b^3 в) 5y-10y^2 б) x^2-9 21b 2y-1 3x-9...
полина10092003 полина10092003  21.05.2019 02:00
Для функции f(x)=3^2+1 найти первообразную, график которой проходит через точку m(1; -2)...
ника2752 ника2752  21.05.2019 02:00
Скорость товарного поезда на 40км\ч меньше скорости пассажирского.товарный поезд за 7 часов проходит такое же расстояние как пассажирский за 4,2 часа.найдите скорость...
dfyz2 dfyz2  21.05.2019 02:00
Расстояние от пункта а до пункта в автобус должен был проехать со скоростью 60 км в час.однако на середине пути он задержался на 30 мин и,чтобы прибыть в пункт в без...
Ученик2281337228 Ученик2281337228  21.05.2019 02:00
Пстройте график функции y=2x-6.с графика найдите: a)наибольшее и наименьшие значения функции на отрезке [-1,2] б)значения аргумента, при которых y=0; y 0...
leylakhalimova leylakhalimova  21.05.2019 02:10
Представьте в виде дроби *заранее признателен.)* a) b-a + b-a б) x^2 + 2x^2 ab b^2 x-2...
Helenar2212 Helenar2212  22.09.2019 17:50
Bво второй и всё это в четвертой / на bв 5...
vasiljev255 vasiljev255  22.09.2019 17:50
Решите уравнение и сделайте проверку 1) -2*(х-1)+3х=7 2) 5у-(3-у)+(2у-1)=у+3 3)2*(х-5)-3*(х+4)=х-22...
ХацуноМико ХацуноМико  22.09.2019 17:50
Знайти різницю арифметичної прогресії, якщо а2=-3, а6=3...

Популярные вопросы