Решите систему уравнений 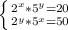 Решение задач должно содержать полное объяснение, записанное в виде последовательных логических действий, со ссылкой на математические факты, из которых следует то или иное утверждение.
Решение задач должно содержать полное объяснение, записанное в виде последовательных логических действий, со ссылкой на математические факты, из которых следует то или иное утверждение.
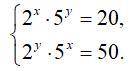
Другие вопросы по теме Алгебра
Популярные вопросы
- Как изменяется внутренняя энергия при переходах твердое вещество...
3 - Вынесите общий множитель за скобки ...
3 - Как правильно следующие слова : северо-западный герлинка птенцов...
1 - Зачем египтяне строили пирамиды 3 причины заранее...
3 - Самолёт, скорость которого относительно воздуха равна 300 км/ч летит...
1 - Сократите дробь 21/360,35/700,54/900,24/600,48/800,75/1000...
1 - Решить все! краткое обьяснения тоже можно, желательно с рисунком....
2 - сочинение! что значит для тебя супер герой! 4-5 предложений! ...
1 - Запишите все правильные дроби, знаменатель которых является наименьшим...
2 - Те,кто решил поступить на ветеринара после 9 класса или уже поступили,можете...
1
Разделим левую часть на левую; правую на правую. получим
(2/5)ˣ*(5/2)^(y)=20/50; после упрощения
(2/5)^(х-у)=2/5⇒х-у=1; х=у+1; подставим, например в первое уравнение, получим 2^(y+1)*5^y=20; (2*5)^y=20/2 ;10^y=10⇒ у=1, подставим в первое уравнение, получим (2)ˣ*5¹=20; 2ˣ=20/5=4=2²; х=2
ответ (2;1)
хотя ответ и прорисовывался с первого взгляда. решил досконально изложить.)
х = 2
у = 1
Объяснение:
I
первое уравнение равняется 20, 5^2 > 20 поэтому нам подойдет 5^1 а не 5^2 и больше, таким образом находим что х = 1.
20:5 = 4
находим первый множитель, и воспользовавшись логарифмом находим степень первого множителя.
II
5^3 > 50
5^1 нам не подойдет потому что 50:5=10 а для двойки нет такой степени которая в результате дала бы 10
поэтому нам подходит 5^2, таким образом ещё раз находим что х = 1.
50:25 =2
опять воспользовавшись логарифмом находим что у = 1.