Решите систему уравнений методам подстановки 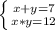
Другие вопросы по теме Алгебра
Популярные вопросы
- Перечислите основные признаки феодального строя...
2 - Втреугольнике abc угол a равен 75, а величина угла b на 12 меньше....
2 - Сравни больше меньше или равно 76мм и 6см , 6см5мм и 7см, 4см и...
1 - Задана пропорция х: 6=30: у найдите значение х и у...
1 - Реши примеры дополнения до 10ти. 8+7. 9+6. 7+5. 8+6. 9+5 образец:...
1 - Если каждый мальчик принесёт 5 кг макулатуры, а каждая девочка...
2 - Нужно проект сделать. нужно описать 3 животных например кошка,собака...
3 - Сколькими нулями заканчивается произведение всех натуральных чисел...
1 - Белоруская . дайте 3 загадки на темы чалавек, частки яго цела\...
3 - Вравнобокой трапеции сумма углов при меньшем основании равна 124...
2
Решим второе уравнение отдельно
Последовательно подставим в первое уравнение
Если x = 3, то y = 4, если x = 4, то y = 3
ответом будет две пары чисел.
ответ: (3;4) и (4;3)
Объяснение:
ответ: (3;4), (4;3).