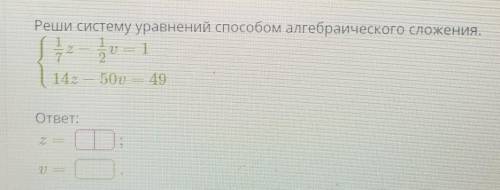
Решите систему уравнений алгебраического сложения ​

Решение системы уравнений v=49;  z=178,5.

Объяснение:

Решить систему уравнений алгебраического сложения:

z/7-v/2=1

14z-50v=49

Умножим первое уравнение на 14, чтобы избавиться от дроби:

2z-7v=14

14z-50v=49

Смысл метода алгебраического сложения в том, чтобы при сложении уравнений одно неизвестное взаимно уничтожилось. То есть, чтобы коэффициенты при неизвестном каком-то были одинаковыми, но с противоположными знаками. Для того, чтобы этого добиться, преобразовывают уравнения, можно умножать обе части уравнения на одно и то же число, делить.

В данной системе нужно первое уравнение умножить на -7:

-14z+49v= -98

14z-50v=49

Складываем уравнения:

-14z+14z+49v-50v= -98+49

-v= -49

v=49

Теперь подставляем значение v в любое из двух уравнений системы и вычисляем z:

14z-50v=49

14z=49+50v

14z=49+50*49

14z=49+2450

14z=2499

z=2499/14

z=178,5

Решение системы уравнений v=49;  z=178,5.