Решите систему уравнений а), \{ {{xy=1} \atop {y=-2x+2}} \right. \left \{ {{xy=8} \atop {y+1=x^{2} }} \right.[/tex][/tex]
Другие вопросы по теме Алгебра
Популярные вопросы
- Вопросы для повторения и задания биология 9 класс мамонтов Захаров стр 22...
2 - Масова частка елементу 2 групи в його хлориді становить 36,04%. Треба знайти назву...
3 - Решите 1,3 упражнение )физика 10 класс) ...
3 - -(4x-3)=-x как решить уравнение...
1 - Запишите в процентах десятичные дроби: 0.87; 0.07; 1.45; 0.035; 2.272....
2 - 1) 67,2:12=? 2) 22,23:19=? 3) 86,5:25=? 4) 4,34:7=? 5) 17:14=? 6) 2:5=? ...
2 - нужен мини доклад по теме роль старославянизмов в современном языке БУДУ ОЧЕНЬ...
2 - До ть будь ласка дуже треба 2. Пригадайте міфи різних народів про виникнення світу....
2 - написать пословицу теме моя родина.и подчеркнуть гласные...
1 - 3.6 На плоскости провели 10 прямых, только две из которых параллельны. Вскольких...
3
P.S. Уравнение 3 степени имеет один действительный корень (2,1663) и два комплексных (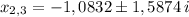 ).
).