Решите систему уравнений
{4 ⁴√x-⁴√y=2√2
{2 ⁴√x+3 ⁴√y=8√2
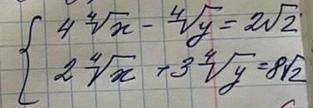
Другие вопросы по теме Алгебра
Популярные вопросы
- 1.прочитайте предложения из сказок а. с. пушкина, выделяя интонацией...
2 - Моє ставлення до роду міщенків та кулаківських пліззік на завтра...
3 - Жанр ,тема девочка на шаре .составить план....
3 - Решите уравнение с решением -5+16х=10-8х...
3 - Органы движения брюхоногих, двустворчатых, головоногих...
3 - Сочинение про кремль легкое и короткое на...
1 - Кто был таким всеволод большое гнездо кратко...
1 - Маленький доклад о петре чайковском нужно на музыку до среды...
2 - Запишіть множину цифр, якими записують дату вашого народження/запишите...
1 - Славяно-греко-латинская академия в москве была открыта...
2
Пусть u = ⁴√x и v = ⁴√y. Тогда первое уравнение системы можно записать в виде:
4u - 4v = 2√2 (1)
А второе уравнение будет выглядеть так:
2u + 3v = 8√2 (2)
Теперь мы можем решить систему методом подстановки следующим образом:
1. Из уравнения (1) выразим одну из переменных через другую. Например, выразим u:
u = (2v + 2 √2 ) / 4 (3)
2. Подставим значение u из уравнения (3) в уравнение (2):
2((2v + 2 √2 ) / 4) + 3v = 8√2
Упростим выражение:
(2v + 2 √2)/2 + 3v = 8√2
v + √2 + 3v = 8√2
4v + √2 = 8√2
3v = 7√2
v = 7√2/3
3. Теперь, имея значение v, можем найти значение u, подставив его в уравнение (3):
u = (2(7√2/3) + 2 √2 ) / 4
u = (14√2/3 + 2 √2) / 4
u = (7√2/3 + √2/3) / 2
u = 7√2 / 3 / 2 + √2/3 / 2
u = 7√2/6 + √2/6
u = (7√2 + √2) / 6
u = 8√2 / 6
u = 4√2 / 3
4. Теперь, когда мы найдем значения переменных u и v, можем найти x и y. Для этого подставим значения u и v в исходные уравнения:
x = u^4 = (4√2 / 3)^4
x = (4^4 * (√2)^4) / (3^4)
x = 256 * 2 / 81
x = 512 / 81
y = v^4 = (7√2 / 3)^4
y = (7^4 * (√2)^4) / (3^4)
y = 2401 * 2 / 81
y = 4802 / 81
Таким образом, решение системы уравнений будет:
x = 512 / 81
y = 4802 / 81