1. Алгебра
  2. Решите систему уравнений

Решите систему уравнений 3x+y=10 x^2-y=8

ВераПончик ВераПончик    1   13.07.2019 02:40    25

Ответы
HaosG HaosG  03.10.2020 02:27

\tt\displaystyle \left \{ {{3x+y=10} \atop {x^2-y=8}} \right. \Longrightarrow \left \{ {{y=10-3x} \atop {x^2-y=8}} \right. \Longrightarrow \left \{ {{y=10-3x} \atop {x^2-y=8}}} \right.

Решим методом подстановки.

\tt\displaystyle x^2-(10-3x)=8\\x^2-10+3x-8=0\\x^2+3x-18=0\\D=3^2-4*1*(-18)=9+72=81\\\sqrt{81}=9\\\\x_1=\frac{-3-9}{2}=\frac{-12}{2}=-6\\\\x_2=\frac{-3+9}{2}=\frac{6}{2}=3

Находим y.

y=10-3x\\\\y_1=10-3*(-6)=10+18=28\\y_2=10-3*3=10-9=1

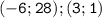
ответ: \tt\displaystyle (-6;28);(3;1)

ПОКАЗАТЬ ОТВЕТЫ
nini8523 nini8523  03.10.2020 02:27

(-6; 28), (3;1).

Объяснение:

\left \{ \begin{array}{lcl} {{3x+y=10,} \\ {x^{2} -y=8;}} \end{array} \right.\Leftrightarrow\left \{ \begin{array}{lcl} {{3x+y=10} \\ {x^{2} +3x=18;}} \end{array} \right.\Leftrightarrow\left \{ \begin{array}{lcl} {{3x+y=10} \\ {x^{2} +3x-18=0.}} \end{array} \right.

Решим квадратное уравнение:

x^{2} +3x-18=0;\\D= 9- 4*1*(-18)= 9+72=810, \sqrt{D} =9;\\\left [ \begin{array}{lcl} {{x=\frac{-3-9}{2} ,} \\\\ {x=\frac{-3+9}{2} ;}} \end{array} \right.\Leftrightarrow \left [ \begin{array}{lcl} {{x=-6,} \\ {x=3.}} \end{array} \right.

Если x=3, то y=10-3*3= 10-9 =1 ;

(3;1)- решение системы

Если x= -6, то  y=10-3*(-6) =10+18=28;

(-6; 28) - решение системы.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Арендатор84 Арендатор84  05.09.2019 10:30
Разложите на множители квадратный трехчлен a) x²-2x-63, б) 5x²-30x+35, в) 17x²-45 15 б...
егорка158 егорка158  05.09.2019 10:30
(m-2)(m-2) -m(4-m) доказать неравенство m - любое натуральное число...
dariyakazakova1 dariyakazakova1  05.09.2019 10:30
Найдите область определения функции 4√х-5...
axmet2 axmet2  05.09.2019 10:30
Основание равнобедренного треугольника на 8 см длиннее его боковой стороны. найти стороны треугольника, если его периметр равен 113 см. выберите один ответ: основание...
dgafar27oy9omz dgafar27oy9omz  05.09.2019 10:30
1)10^2-3^2 2)(10-3)^2 3)-)^6 4)-7^3+(-2)^3 5)0,2×3^2-0,3×2^4 6)8×0,5^3+25×0,2^2...
StarBoy12ewq StarBoy12ewq  05.09.2019 10:30
2x-3): 3 = (4x-1): 5 решить уравнение...
МудраяСоваАлександра МудраяСоваАлександра  05.09.2019 10:30
36c-3(5-6c)2 (7b-1)(1=7b)-b(4-3b) (2k-3)(3+-5)2-30k решить уровнения 1)x2-(x+4)=2x 2) (3y+1)2-9(y-1)=8y-16...
PahaBroZ PahaBroZ  25.06.2019 11:40
Найти сумму пятидесяти первых нечетных натуральных чисел...
simono627122va simono627122va  25.06.2019 11:40
Разложить многочлен на множители: p³ + (3p - 4)³...
BirdNumber1 BirdNumber1  25.06.2019 11:30
Известно, что x^4=y^4 и (y-1)=4. чему не может равняться x...

Популярные вопросы