Решите систему уравнений:
{2x + y = 4,
{xy + 2х = -12.
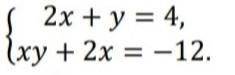
Другие вопросы по теме Алгебра
Популярные вопросы
- Завтра важная самостоятельная. со 2 вариантом (и если не сложно, то...
2 - кофта стоила 200 грн затем цена снизилась на 15% сколько теперь она...
1 - Опишите фазовый переход кристаллизация (отвердевание) и раскройте его...
2 - Эссе как учиться самостоятельно ...
3 - Написать глаголы, причастия и деепричастия с не (слитно и раздельно....
1 - 483. начертите координатный луч с единичным отрезком, равным6 см. отметьте...
1 - Вычеслите 1) 2/3: (-2); 2) 4: (-1/2); 3) (-5/6): (-5/12); 4) (-4 2/3):...
3 - Вкоробках по 1 красному шару и остальные синие. в первой 15 шаров,во...
2 - Какие общие свойства у кристаллогидратов? ...
3 - 8. автобус рухається зі швидкістю 54 км/год. побудуйте графік шляхуавтобуса...
1
Объяснение:
{2x + y = 4, (1)
{xy + 2х = -12. (2)
Из (1) у=4-2х;
Подставляем в (2):
х(4-2х) = -12;
4х - 2х² + 12=0; [: -2]
x² -2x -6 = 0;
x1= 3.64; x2= -1.64;
Подставляем
х1=3,64;
у= 4-2*3,64;
у1= -3,28;
при x2 = -1.64
y=4-2*(-1.64)
y2= 7.28.
Система уравнений имеет вид:
1) 2x + y = 4
2) xy + 2x = -12
Для начала, давайте умножим первое уравнение на 2, чтобы избавиться от коэффициента 2 перед переменной x. Получим:
3) 4x + 2y = 8
Теперь сложим уравнения 2) и 3):
4) (xy + 2x) + (4x + 2y) = -12 + 8
Приведём подобные слагаемые:
5) xy + 4x + 2x + 2y = -4
Упростим:
6) xy + 6x + 2y = -4
Теперь давайте из первого уравнения выразим переменную y. Вычтем из уравнения 1) 2x, получим:
7) y = 4 - 2x
Подставим значение y = 4 - 2x в уравнение 6):
xy + 6x + 2(4 - 2x) = -4
Раскроем скобки:
xy + 6x + 8 - 4x = -4
Сгруппируем переменные x и у:
xy - 4x + 6x = -4 - 8
Упростим:
xy + 2x = -12
Получили уравнение 2), которое уже имеется в системе. Значит, система имеет бесконечное количество решений.
Давайте найдем значения переменных x и y. Подставим выражение для y из уравнения 7) в уравнение 1):
2x + (4 - 2x) = 4
Раскроем скобки:
2x + 4 - 2x = 4
Сгруппируем переменные x:
2x - 2x + 4 = 4
Упростим:
4 = 4
Получили верное равенство. Значит, всякие значения переменной х, при которых x - любое число, будут являться решениями данной системы уравнений.
Таким образом, ответом на данную систему уравнений является:
x - любое число
y = 4 - 2x