Решите систему уравнений
1){x²+7xy=-6
9y²-xy=10
2)x³y³-x²y⁴=-54
x⁴y²-x³y³=-18
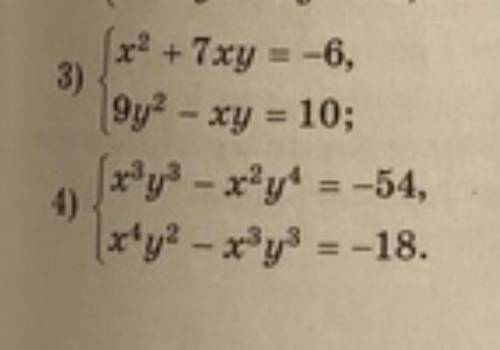
Другие вопросы по теме Алгебра
Популярные вопросы
- Земледелие, при котором не используют минеральные удобрения и средства...
2 - Не могу решить ромб диагонали которого имеют длины равные 6 и 4,8 имеет...
2 - Маленькая сказка про дикорастущие растения или фрукты...
2 - Complete the sentences. use the infinitive or -ing form and true information...
2 - Дайте определение: исскуственный отбор,борьба за существование,естественый...
1 - Выпишите из кубок (жуковского) метафоры,эпитеты ,сравнения и олицетворения....
2 - 1)почему в начале тренировок происходит значительное улучшение спортивных...
2 - Вопросы по сказке черная курица или подземные жители а. погорельский...
1 - 1)расскажите об основных направлениях и принципах организации торговли...
3 - Разделите смесь состоящая из сахара, мела, воды, железных опилок. опишите...
3
1) Решение системы уравнений:
Уравнение 1: x²+7xy=-6
Уравнение 2: 9y²-xy=10
Для начала выразим переменную y из уравнения 2 и подставим ее в уравнение 1:
9y²-xy=10 => y² = (10+xy)/9 => y = ±√[(10+xy)/9]
Подставляем выражение для y в уравнение 1:
x²+7x(±√[(10+xy)/9]) = -6
Данное уравнение является квадратным относительно переменной x. Решим его с помощью квадратного трехчлена.
Выносим общий множитель x из выражения:
x( x+7√[(10+xy)/9]) = -6
Теперь мы имеем две возможности:
1. x = 0
2. x+7√[(10+xy)/9] = -6
Если x = 0, то подставляем это значение во второе уравнение:
9y²-0y=10 => y = ±√(10/9)
Таким образом, получаем два решения для первой системы уравнений:
Решение 1: x = 0, y = ±√(10/9)
Рассмотрим вторую возможность:
x+7√[(10+xy)/9] = -6
Теперь выразим x из этого уравнения:
x = -6 - 7√[(10+xy)/9]
Подставляем это значение x в уравнение 2:
9y²-(-6 - 7√[(10y+xyy)/9])y = 10
Упрощаем:
9y² + 6y + 7√[(10y+xyy)/9]y - 10 = 0
После этого уравнение будет содержать только переменную y. Решим его с помощью квадратного трехчлена.
Теперь у нас есть два решения для системы уравнений:
Решение 2: x = -6 - 7√[(10y+xyy)/9], y - корень выражения после решения уравнения.
2) Решение системы уравнений:
Уравнение 1: x³y³-x²y⁴=-54
Уравнение 2: x⁴y²-x³y³=-18
Для удобства заменим переменные: u = x² и v = y².
Перепишем систему уравнений:
u²v³ - uy⁴ = -54 (уравнение 1)
uv² - u²v³ = -18 (уравнение 2)
Добавим уравнения, чтобы убрать u²v³:
u²v³ - uy⁴ + uv² - u²v³ = -54 - 18
- uy⁴ + uv² = -72.
Упростим:
uv² - uy⁴ = -72
Теперь решим это уравнение относительно u. Выразим u через v и y:
u = v / (v - y⁴)
Подставим это значение u в уравнение 2:
(v / (v - y⁴))v² - (v / (v - y⁴))y⁴ = -72
Упростим:
v³ - vy⁴ - (v²y⁴) / (v - y⁴) = -72 (уравнение 1)
v / (v - y⁴) = 72 / (vy⁴ + 1) (уравнение 2)
Обратим внимание, что знаменатель уравнения 2, это разность куба и четвертой степени y. Рассмотрим следующие случаи:
1. y⁴ ≠ v
Если y⁴ ≠ v, то v = 72 / (vy⁴ + 1)
2. y⁴ = v
Если y⁴ = v, то v = 0 (подставляем это значение в уравнение 1 и получаем тождество)
Таким образом, получаем два решения для второй системы уравнений:
Решение 1: v = 72 / (vy⁴ + 1), y - любое значение, кроме корня v
Решение 2: v = 0, y - любая действительная переменная
Надеюсь, это подробное объяснение помогло вам понять решение поставленной системы уравнений. Если у вас остались вопросы, пожалуйста, дайте знать.