Решите систему тригонометрических уравнений и запишите количество решений на заданном промежутке
Другие вопросы по теме Алгебра
Популярные вопросы
- 1. write positive or negative sentences. use am/am not, is/isn’t,...
1 - Сравни по размеру тигра и кошку ,кошку и мышку...
3 - Написать правильно слова разже(ч/чь)пе(ч/чь)испе(ч/чь)кули(ч/чь)но(ж/жь)отре(ж/жь)кусоч-к.съе(ш/шь)читае(ш/шь)не...
1 - Вдетской книжке было 183 цифр (начиная с первой). сколько страниц...
1 - Відредагуйте словосполучення, уникаючи тавтології та плеоназму. руйнівний...
1 - (9,1-х)-2,8=2,9 люди добрые за 5 минут...
3 - Примеры дружбы из рассказа в.п.астафьева фотография, на которой меня...
1 - Запишите глагольные формы : кричать, сгореть, говорить....
2 - Из кололы в 36 карт надо вытащитт 4 карты так что бы среди них был...
1 - Всем ) нужно открыть копилку с гипсовым дном! как это сделать? в...
3
5
Объяснение:
Из второго уравнения следует, что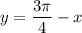 . Подставим в первое уравнение:
. Подставим в первое уравнение:
Найдём количество решений с системы неравенств:
При заданных условиях система имеет 5 решений.