Решите систему тригонометрических неравенств:
tgx-siny=3
tg^2x+sin^2y=17
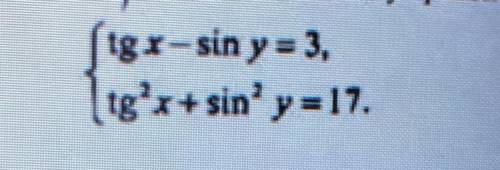
Другие вопросы по теме Алгебра
Популярные вопросы
- Қазақстан еуразиялық кеңістіктің мәдени бесігі 6 неліктен әдісімен диалог құрау...
1 - Собрали 30 кг клубники после того как из части ягодсварили варенье и 14 кгзамарозили...
3 - Сдвух ульев за год получили 78кг мёда . с одного из них получили 43кг. на сколько...
3 - Что делать если случилась авария на взлёте? , можно коротко...
1 - Состав равенства и неравнства исползуя выражения на карточках 6×3 8×4 9×4 2×9...
3 - (10 ! ) сделать сравнительную характеристику маруси и сони из произведения в....
2 - What did they call gulliver? перевод нужен...
2 - 6-4x=4-6(x-7) решить. сомневаюсь в ответе...
1 - Земельный участок имеет форму прямоугольника. одна сторона равна 31 м 6 дм ,...
2 - Выбери из этих растений крестоцветные: свекла, репа, редис, морковь, капуста,...
2
tg^2x + sin^2y = 1.
Тогда у нас будет следующая система уравнений:
tgx - siny = 3.
tg^2x + sin^2y = 1.
Давайте решим эту систему методом последовательных приближений. Предположим, что синус и тангенс угла неотрицательны. Вы можете проверить это изначальное предположение, используя графикы функций синуса и тангенса.
1. Подставим в первое уравнение выражение для синуса через косинус:
tgx - sqrt(1 - cos^2y) = 3.
2. Заменим тангенс через синус и косинус:
sinx / cosx - sqrt(1 - cos^2y) = 3.
3. Переформулируем уравнение, чтобы оставить только синусы:
(1 - cos^2x) / cosx - sqrt(1 - cos^2y) = 3.
4. Выразим косинусы через синусы с помощью тригонометрической тождественности (1 - sin^2x) = cos^2x:
(1 - sin^2x) / sqrt(1 - sin^2x) - sqrt(1 - cos^2y) = 3.
5. Упростим уравнение:
1 / sqrt(1 - sin^2x) - sqrt(1 - cos^2y) = 3.
6. Заменим оставшийся корень на синус и косинус:
1 / cosx - sin(90° - y) = 3.
7. Умножим оба выражения на cosx:
1 - sinx*cos(90° - y) = 3*cosx.
8. Используем тригонометрическую тождественность sin(90° - x) = cosx:
1 - sinx*siny = 3*cosx.
Теперь у нас есть система уравнений:
tgx - siny = 3,
1 - sinx*siny = 3*cosx.
Давайте решим ее. Сначала из второго уравнения выразим sinx:
sinx = (1 - 3*cosx) / siny.
Подставим это выражение в первое уравнение:
tgx - siny = 3.
tgx - siny = 3.
tgx - siny = (3 - (1 - 3*cosx) / siny).
^.3.5(3 - (1 - 3*cosx) / siny).
^.5(3siny - (1 - 3*cosx)) / siny.
^.5(3siny - 1 + 3*cosx) / siny.
^.1.5(3siny - 1 + 3*cosx).
*.siny.
3siny^2 - siny + 3*sinxcosx = 1.5siny,
3siny^2 - 2.5siny + 3*sinxcosx - 1 = 0.
Перепишем данное уравнение в виде квадратного уравнения относительно siny:
3siny^2 - 2.5siny + 3*sinxcosx - 1 = 0.
siny^2 - (2.5/3)siny + (1 - 3*sinxcosx/3) = 0.
siny^2 - (5/6)siny + (1 - sinxcosx) = 0.
Теперь у нас есть квадратное уравнение относительно siny. Давайте решим его, используя дискриминант:
D = (5/6)^2 - 4(1)(1 - sinxcosx).
D = 25/36 - 4 + 4sinxcosx.
D = 25/36 - 4 + 4sinxcosx.
D = 25/36 - 144/36 + 4sinxcosx.
D = -119/36 + 4sinxcosx.
Так как D < 0, то в системе нет решений.
Ответ: данная система тригонометрических неравенств не имеет решений.