Решите систему тригонометрических неравенств cos(x)>=корень из 2/2 sin(2x)<-0.5
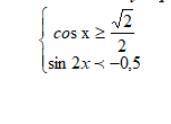
Другие вопросы по теме Алгебра
Популярные вопросы
- Приведите подобные слагаемые 8х+3у-6х-5у...
3 - Расставь в порядке возрастания...
3 - Помагите по математик очень нужна с 1.68 по 1.72 и с 1.103 по 1.107 помажааалуйстаа...
2 - с физикой ТЖБ 1 токсан отинем...
1 - Сравните характерные черты развития Чехии и Польши в XVI - XVII в.в....
3 - Если одна буква в слове отображена красной буквой то Какого цвета будут...
3 - до 120 мл суміші водного і азотного р-ну додали 150 мл кисню і запалили...
3 - Какую религию исповедовали хунны...
2 - Пряма FE не належить площині AOB. Скільки спільних точок мають площини...
1 - Напишите свое мнение о романе Знак Кассандры .Напишите свое мнение о...
1
рисунок1
рисунок2
рисунок3
Пересекаем оба решения (на 1 рис и 3 рис)
рисунок 4
n принадлежит Z.