Решите систему неравенств
x^2+y^2>=25 (x²+y²≥25)
x+y<9
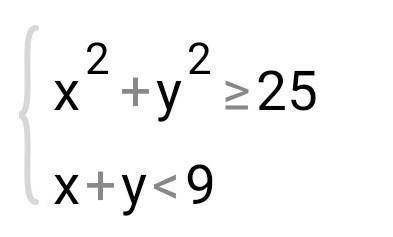
Другие вопросы по теме Алгебра
Популярные вопросы
- П ять прикладів переживань коли відчуваєш страх гнів любов ненависть...
1 - Нужно словесно описать интерьер своей комнаты в 1 предложении...
1 - Решите уравнение а)5 3/8х=-1 11/32 б)2 4/7х=36/49 в)-0,73х=0,7738...
1 - Придумайте 5 по теме решение и решите их...
1 - Сторона bc треугольника abc на 5 см больше его стороны ab, а сторона...
2 - Уайда карандашей в 3 раза меньше чем ручек. сколько карандашей у айда...
3 - Oпишите вашу любимую игрушку используя синонимы. , ничего в голову...
2 - Длина стрелки наручных часов равна 10 мм. а)чему равен период стрелки...
1 - Непонятна тема числовые выражения, содержащие квадратный корень ....
2 - Синтаксический разбор предложения солнце пробивалось сквозь ветви...
2
Это неравенство представляет собой уравнение окружности с центром в начале координат и радиусом 5. Окружность включает в себя все точки, находящиеся на и вне окружности.
Теперь рассмотрим второе неравенство x + y < 9.
Мы можем представить это неравенство в виде линии на плоскости, где x + y = 9 является уравнением этой линии. Линия разделяет плоскость на две области: одна область под линией, где x + y < 9, и другая область над линией, где x + y > 9.
Теперь нам нужно найти пересечение областей, представленных обоими неравенствами. Для этого нарисуем оба графика на одной координатной плоскости.
На рисунке можно увидеть, что область, удовлетворяющая обоим неравенствам, это область, находящаяся под окружностью x^2 + y^2 ≥ 25 и слева от линии x + y = 9.
Решением системы неравенств будет любая точка, которая находится в этой области. Точки на окружности и на линии не включаются в решение, так как равенство в неравенствах не выполняется.
Следовательно, решение системы неравенств это все точки (x, y), которые удовлетворяют условию:
x^2 + y^2 ≥ 25 (точки внутри и на окружности)
x + y < 9 (точки под линией x + y = 9)
Таким образом, решение системы неравенств представляет собой область на плоскости, которая не включает в себя окружность и лежит под линией x + y = 9.