Алгебра: Решите систему неравенств у меня соч

Решите систему неравенств у меня соч

Ответы

Dlana 13.06.2021 14:51

Решим первое неравенство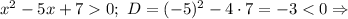 $x^2-5x+70;\ D=(-5)^2-4\cdot 7=-3$

соответствующее уравнение корней не имеет, а поскольку старший коэффициент =1>0,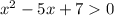 x^2-5x+70 при всех x.

Остается решить второе неравенство. Существует много рассуждения, выберем тот , который редко используется. Поскольку обе части неравенства неотрицательны, извлечение корня из них приводит к равносильному неравенству

$|x|\le 9,$

остается вспомнить геометрический смысл модуля, состоящий в том, что модуль x - это расстояние от начала координат до точки с координатой x. Поэтому $|x|\le 9\Leftrightarrow x\in [-9;9].$

ответ: [- 9;9]

ПОКАЗАТЬ ОТВЕТЫ

Mamiksem 13.06.2021 14:51

$x \in[-9; \: 9]$

Объяснение:

$\begin{cases} {x}^{2} - 5x + 7 0 \: \: \big |^{7 =6{,}25 + 0{,}75 } _{5x =2 \cdot2{,}5x } \\ {x}^{2} \leqslant 81 \end{cases} \\ \begin{cases} {x}^{2} - 2 \cdot2{,}5x + 6{,}25 + 0{,}75 0 \\ |x| \leqslant \sqrt{81} \end{cases} \\ \begin{cases}( {x}- 2{,}5)^{2} + 0{,}75 0 \: \small{< = x \in } \: R\\ |x| \leqslant \sqrt{81} \end{cases} \\ \begin{cases}x \in \R\\ - 9 \leqslant x \leqslant 9 \end{cases} \: < = \begin{cases} x \in \R\\x \in[-9; \: 9] \end{cases} \\ x \in[-9; \: 9]$