Решите показательные уравнения
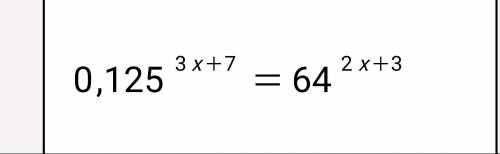
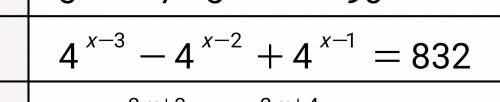
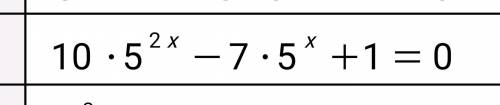
Другие вопросы по теме Алгебра
Популярные вопросы
- Придумать интересный вопрос по языку для 4-класса...
1 - Қазақстанда қандай үлкен таулар бар?...
1 - На решение двух васе потребовалось 42 минуты а на решение трёх примеров на...
1 - Разабрать по чл предложения, и частям речи . ранним утром ты едешь в соседнюю...
3 - Расскажите о сферах влияния бога тенгри , богини умай и бога уббе...
3 - Определить питание рек: лена, колыма, сырдарья, амур, нил, замбези, яну...
3 - Какое из чисел является корнем уравнения y+322=351 1 выберите правильный ответ:...
1 - Сообщение экологии проблем нашиво края села георгивского...
3 - Выполните умножение смешанных чисел 7 1/2*2 4/15; 5 1/6*3 1/7; 3 3/7*2 1/3;...
1 - Мальчик хочет купить несколько пачек мороженого пр 8р., но у него только 5-...
3
Надеюсь всё хорошо видно)
Объяснение:
1)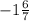
2) 6
3) x₁=-㏒₅2; x₂=-1
Объяснение:
1)
2)
3)
Пусть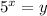 тогда:
тогда:
Подставляем значения y:
x₁=-㏒₅2; x₂=-1