Решите показательные неравенства. 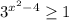
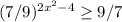
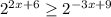
Другие вопросы по теме Алгебра
Популярные вопросы
- В столовой за неделю израсходовали 28 кг масла, поровну каждый...
1 - Сторона квадрата 9 см. Найди периметр и площадь этого квадрата....
3 - Лисица и барсук убегают друг от друга от одной норы в противоположных...
1 - Скорость удаления двух машин равна 170 км/ч. С какими скоростями...
3 - От одного автовокзала вышли одновременно в противоположных направлениях...
3 - Вычисли. 95 т 35 кг – 68 т 29 кг 56 т 9 ц + 33 т 2 ц 44 кг 132...
1 - Вычисли. 890 км 456 м – 48 км 398 м 2 м – 13 см 67 дм 48 см +...
3 - Два вертолёта вылетели с аэродрома в противоположных направлениях....
3 - Найди площадь квадрата с длиной стороны 1/10 м....
3 - Четыре трактора обработали 1700 га земли поровну каждый. Сколько...
1
Объяснение:
ответ: х принадлежит (-беск;-2]U[2;+ беск).
так как основание < 1, знак меняется.
х принадлежит