Решите параметр (4 задание).

Система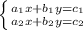       не имеет решений, если коэффициенты при неизвестных пропорциональны, но не пропорциональны свободным членам:

Значит, в данной системе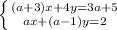  

1) должно выполняться равенство:

По теореме Виета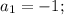      

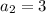
2) и не должно выполняться равенство:

3)  и не должно выполняться еще одно равенство:

Получается, что у данной системы решений нет при  и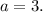  

ответ: {-1;  3}