Решите неравенство
0<x+√(x+2)
​

ОДЗ: ;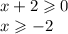

Рассмотрим 2 случая:

1) :

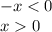В данном случае получаем отрицательную правую часть уравнения. В левой же части – корень и он больше отрицательного числа всегда, когда существует, поэтому в данном случае .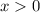

2) :

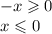Теперь же как в левой части так и в правой неотрицательные числа, поэтому можно возводить в квадрат обе части уравнения:

Так как в данном случае у нас стоит ограничение на х ≤ 0, то ответом есть .

Осталось объединить полученные ответы:

ответ: .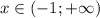

ответ: (1;+∞)

Объяснение: