Решите неравенство -во вложении
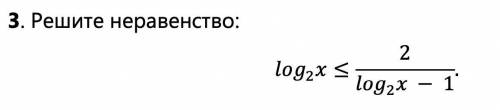
Другие вопросы по теме Алгебра
Популярные вопросы
- ОЧЕНЬ Какую массу соли можно получить при реакции 76г 10%-го...
1 - Запишите разность выражения и у результат1) m-n и n-m2) 45-k...
1 - Из предложенных утверждений выберите определение дисперсии А)...
3 - Какие мировые области стока(бассейны) разделяет этот водораздел?(про...
2 - Задание 1 Является ли равенство a5+a18=a23 тождеством? Докажи....
3 - Выберите правильные времена глагола: a. have studied; b. had...
3 - Напишите ход решения: (1+i)^8 тема - комплексно сопряженные...
3 - Прия кому значені n вектори a (-3;4-2) b (n;-4;2) будуть колінеарні,...
1 - Какую правду обещал шептать перед смертью собаки антипыч...
3 - решить пример по математике...
3
log(2) x ≤ 2/(log(2) x - 1)
одз x > 0
log(2) x ≠ 1 x ≠ 2
x ∈ (0,2) U (2,+∞)
Замену сделаем для простоты и наглядности
log(2) x = y
y ≤ 2/(y - 1)
y - 2/(y - 1) ≤ 0
(y² - y - 2) / (y - 1) ≤ 0
y² - y - 2 = 0
D = 1 + 8 = 3
y12 = (1 +- 3)/2 = 2 -1
(y - 2)(y + 1)/(y - 1) ≤ 0
Метод интервалов
-----------[-1] +++++++ (1) ------------- [2] ++++++++
y ∈ (-∞, -1] U (1, 2]
log(2) x <= -1
x <= 1/2
log(2) x > 1
x > 2
log(2) x ≤ 2
x ≤ 4
+ ОДЗ
x ∈ (0, 1/2] U (2, 4]
Решение на фотографии.
Объяснение:
Если отметь как лучший!)