Решите неравенство: )
Другие вопросы по теме Алгебра
Популярные вопросы
- Словоа с разделительным твердым знаком...
2 - 1). если делимое равно делителю, то частное ровно 2). если делимое равно...
3 - Составить маленький диалог на тему продавец спрашивавет ну сначало здоровается...
1 - Сообщение на тему древнегреческие мифы...
3 - Что такое сила? это величина скалярная или векторная?...
2 - Наступили 3 холода и по утрам 2 лужицы3 покрываются хрупким2 ледком4 разобрать...
1 - Укажите словосочетание в состав которых входят страдательное причастие времени.(а)растаявший...
1 - Вмагазин завезли 700 кг овощей которые были проданы за три дня . в первый...
3 - Кішкене ат пен үлкен ат бір қазыққа байлаулы айналса да мың қабат тілемейді...
2 - Письменно объяснить букву е в корне слова развевается....
3
Преобразуем неравенство: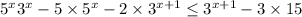
Далее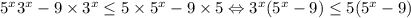 , вынося общий множитель:
, вынося общий множитель:
ответ: фото.
Объяснение: