Решите неравенство ♡♡♡♡♡ решите что сможете♡

Другие вопросы по теме Алгебра
Популярные вопросы
- Распространите назывные предложения, запишите их. родина . простор....
1 - Решить : сколько оборотов сделает минутная стрелка за 2 часа...
1 - Найди в тексте имена прилагательные в форме мн .числа и п п....
3 - Кролики. в сарае у максима кролики. в клетке серые кролики. максим...
2 - Почему платовым были выбраны мастера из тулы для достойнового...
3 - Стих про любую профессию (короткий)...
2 - Подчеркни словосочетания в которых местоимения употреблены вместо...
2 - Различие между силой трения скольжения и покоя?...
3 - Ученику саше дали приготовить 17%-ный раствор гидроксида натрия...
1 - Как выглядел и как город- коммуна?...
3
Объяснение:
-∞__+__-1,5__-__3__+__+∞ ⇒
ответ: x∈(-∞;-1,5)U(3;+∞).
ответ: x∈(-∞;+∞).
ответ: неравенство решения не имеет.
1) -2x²+3x+9≤0
-2x²+6x-3x+9≤0
-2x(x-3)-3(x-3)≤0
(x-3)(2x+3)≥0
ответ: x∈(-∞,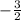 ] ∪ [3,+∞)
] ∪ [3,+∞)
2) 2x²-x+4>0
2x²-x+4=0
x∉R (Дискриминант отрицательный)
т.к. старший кэффициент "a" положительный ⇒ левая часть неравенства всегда положительна
ответ: x∈R
3) -x² +3x-8≥0
-x²+3x-8=0
x∉R (Дискриминант отрицательный)
т.к. старший кэффициент "a" отрицательный ⇒ левая часть неравенства всегда отрицательна
ответ: x∈∅