Алгебра: Решите неравенство методом интервалов. (x-6)(x+9) 0

Если с одной стороны находится произведение нескольких скобок, а с другой -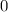 , то мы имеем право применить метод интервалов.Для того, чтобы решить данное неравенство методом интервалов, сначала найдем те значения , которые при подсчете произведения дают 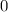.То есть, это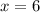 (уравнение 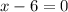) и ().Ставим эти два числа на координатной прямой. Обозначаем их выколотыми точками, так как неравенство строгое. Смотрите рисунок в приложении.Далее выставляем знаки на трех полученных промежутках. Можно, во-первых, выбрать...

Решите неравенство методом интервалов. (x-6)(x+9)<0

Ответы

XMuhamedKinggX 15.10.2020 15:14

ответ с решением на фотографии.

Решите неравенство методом интервалов. (x-6)(x+9)<0

ПОКАЗАТЬ ОТВЕТЫ

NastyTyan 15.10.2020 15:14

Если с одной стороны находится произведение нескольких скобок, а с другой - , то мы имеем право применить метод интервалов.

(x-6)(x+9)

Для того, чтобы решить данное неравенство методом интервалов, сначала найдем те значения , которые при подсчете произведения дают .

То есть, это x=6 (уравнение x-6=0 ) и x=-9 ( x+9=0 ).

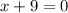Ставим эти два числа на координатной прямой. Обозначаем их выколотыми точками, так как неравенство строгое. Смотрите рисунок в приложении.

Далее выставляем знаки на трех полученных промежутках. Можно, во-первых, выбрать какое-то число из промежутка и проследить за знаком произведения.

А можно обратить внимание на то, что перед нами - квадратичная функция, парабола, ветви которой направлены вверх. Поэтому на "боковых" промежутках произведение положительно (ставим "+"), а на "среднем" промежутке отрицательно (ставим "-").

Так как стоит знак "меньше", то мы берем промежуток посередине и ставим круглые скобки (как уже было оговорено, неравенство строгое). В общем, пишем ответ:

$\large \boxed { x \in (-9 ; \; 6 ) }$