Решите неравенство методом интервалов
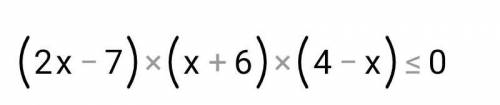
Другие вопросы по теме Алгебра
Популярные вопросы
- Ж.Жабаев кімдермен айтысқан...
2 - с примером по математике. 1 2/9 * 3 2/3 + 4 2/5 : (7/10 + 2 3/5) - (3/17 -...
3 - Найдите функцию, равную пустому члену (-4), которая параллельна графику функции...
3 - Укажите элемент расположенный во втором периоде со степеньями окисления -4,+2,+4...
3 - Вставьте в пропуски глагол to be в правильной форме (am, is, are) ___ the boys...
1 - В положительном ионе гелия находится ... электронов. Вставьте слово...
1 - Вставьте правильный предлог времени - IN, ON или AT 1.His house is near the...
2 - Повесть А.С Пушкина Пиковая дама В чем смысл заключения произведения? Кому...
2 - Всë есть в фото! С 4 заданием где нужно вставить правильный глагол...
1 - Депозитный вклад величиной в 3000 рублей вложен в банк на 6 месяцев при 6 %...
1
Объяснение:
Найдём нули функции:
Определим знаки интервала на промежутках
Неравенство принимает отрицательные или равные нулю значения на промежутках
значит,