Решите неравенство методом интервалов: 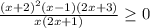
Другие вопросы по теме Алгебра
Популярные вопросы
- Как понять это прочитайте ниже текст. преобразуйте слово, напечатанное...
1 - Скласти речення з словами хуртовина, красивий, плач слухняний....
3 - Этилформиат является продуктом взаимодействия 1) этаналя и метанола...
2 - Вставьте подходящее слово. с транспортёра перемещают различные...
3 - Образ дома в повести шинель . несколько предложений....
1 - Вычисли. 3009×50+7526 17000×3: 100 1650×200-30483...
2 - Зайыр! каламымды подскажите -та полностью продолжение...
2 - (67 т 5 кг - 49 т 8 кг)*5+31 т 6 ц*2= (25*4+9+70)+(200-60+5)+143+(56:...
3 - Решите уравнение: √2х^2-10х=-8√2 , с объяснением...
1 - Определите объем воды,который необходимо взять для приготовления...
2
x ∈ (-∞; -1.5] ∪ (-0.5; 0) ∪ [1; +∞)
Объяснение:
ООФ: x≠ 0, 2х+1 ≠0 ⇒ x ≠ -0.5
(x+2)²(x-1)(2x+3) = 0
(x+2)² ≥ 0 при любом x посему рассмотрим
(x-1)(2x+3) = 0
x = 1
x = -1.5
+ - + - +
.₀₀.
-1.5 -0.5 0 1
x ∈ (-∞; -1.5] ∪ (-0.5; 0) ∪ [1; +∞)