Решите неравенство: 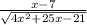 < 0
< 0
Другие вопросы по теме Алгебра
Популярные вопросы
- Какие бывают простые придложения(пп) бывают: восклицательными, невосклицательными,...
3 - Прочитай скороговорки,найди формы слов и однокоренные слова, кукушка...
3 - Изложения деревья ходят. однажды митраша и настя...
3 - Как вы думаете полезно ли уметь разбираться в морфемном составе слова...
2 - Преобразуйте линейное уравнение к виду у=кх+у 7х-9у=11 15х-12у=0 2х+3у=57...
3 - Выписать слово колобок в начальной форме и разобрать как части речи...
3 - Как правильно написать отчества от имен: анатолій, аркадій, валерій,...
1 - Радиус первой окружности равен 2 см ,а радиус второй окружности - 3 см.расстояние...
3 - В3 пакетах 15 грецких орехов. сколько нужно пакетов для 25 грецких орехов?...
1 - Во сколько раз масса коробки с печеньем больше массы коробки с пастилой,если...
1
Объяснение:
Заметим, что подкоренное выражение не может дать отрицательного значения. Тогда перейдем к системе:
Неравенство решено!