Решите неравенство log6(x+4)+log6(x+1)≤2

Другие вопросы по теме Алгебра
Популярные вопросы
- Опишіть фестиваль етнічної музики (коротко)(музика) МНОГО БАЛОВ...
2 - Согласно периодической таблице, какой из электронов натрия и магния,...
3 - Область значений y=(1/4)^x+1...
2 - 102. Существительные какого ряда относятся к одному типу склонения?А)...
3 - Составьте уравнение сторон треугольника, зная его вершину C(4;3), а...
1 - Джури козака Швайки виписати фрази, які ви вважаєте ключовими для розуміння...
2 - Напишите по плану. Дано Доказать Доказательство остался 20 минут до...
1 - 10. Основою суспільства в Месопотамії були:...
1 - упростить выражение и не только...
1 - ОПРЕДЕЛИТЬ ОБЬЕМ СТАЛЬНОЙ ГИРИ МАССОЙ 100Г. УКАЗАНИЕ К РАБОТЕ. 1. Определите...
3
Объяснение:
ОДЗ: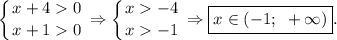
Преобразуем, пользуясь тем, что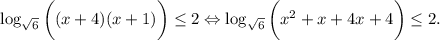
Поскольку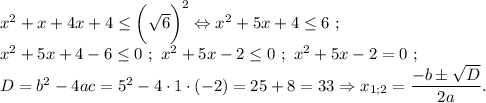
Корни: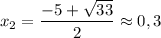 - удовлетворяет ОДЗ.
- удовлетворяет ОДЗ.
ответ с учетом ОДЗ: