Решите неравенство: log x+1 (x-1)*log x+1 (x+2)=< 0
Ответы
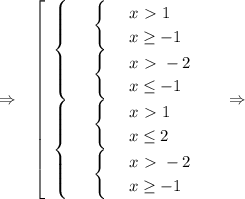
Произведение будет меньше равно нуля, если либо первый множитель ≥ 0 и второй множитель ≤0, либо наоборот.
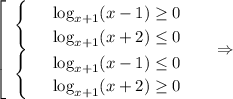
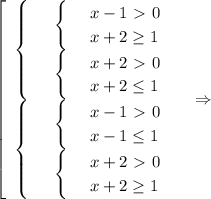
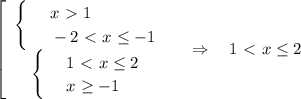
ПОКАЗАТЬ ОТВЕТЫ
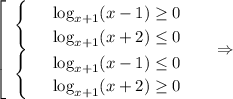
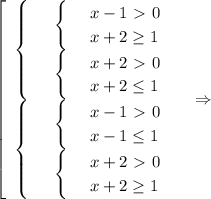

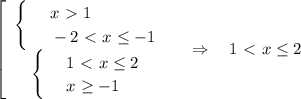
Популярные вопросы
- 3. правительство страны ограничило ввоз бытовой техники ино-странного производства....
3 - Составьте предложение. 1)с однородными членами. 2)с вводным словом. 3)сложное...
1 - 30 за ответ с конечной ! четыре одинаковых сообщающихся сосуда, имеющие площадь...
3 - Образуйте сравнительную и превосходную степени прилагательных good и bad....
1 - Часть горных хребтов в тянь-шаня на территории казахстана...
3 - Объясните пословицу не всякий прут по закону гнут...
3 - Какие игры в детстве воспитываютмужские качества...
3 - Ввыпуклом четырех угольнике abcd угол abd равен углу acd. докажите, что угол...
3 - Усуществительного бывает единственное и множественное число. а какие показатели...
3 - Значение какого из выражений является числом иррациональным? 1) (√5 + √3) * (√5...
3