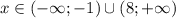Решите неравенство log с основанием 8 (x^2-7x) больше 1
Другие вопросы по теме Алгебра
Популярные вопросы
- В какую точку при повороте на угол 90 ° против часовой стрелки переходит точка...
3 - Рассчитай количество нуклонов, протонов и нейтронов в изотопе химического элемента...
3 - 1 ) х-у-2=0 2х-3у+1=02) -х+у-4=0 4х+у+1=03) 3х+у-4=0 5х+у-10=04) 8х+3у-7=0 3х+у-9=05)х+5у+2=0...
2 - Из формул (H 2 SO 3 , NaCl, Ba(OH) 2 , H 2 O, S, BaO, Ba, SO 2 , HNO 3 , BaSO...
3 - Случайным образом выбрали двузначное число, найдите вероятность того, что оно:...
3 - Из данных предложений выберите и запишите то , в котором есть фразеологизм....
1 - Юрій Іздрик Молитва аналіз. До ть будь ласка. ...
3 - 1.) Знайдіть у тексті речення з модальними дієсловами та їх еквівалентами. Power...
1 - 1. В чем смысл притчи?2. Какой мудрости научил человека отшельник?3. Как зависит...
2 - с казахским языком! Ну прям...
1
log с основанием 8 (x^2-7x) > log 8 8
x^2-7x>8
x^2-7x-8>0
x^2-7x-8=0
D=49+32=81=9^2
x=(7+9)/2 = 8
x=(7-9)/2 = -1
Знаки +/-/+, поэтому решение будет x∈(-∞; -1)∪(8; +∞)
ОТВЕТ: x∈(-∞; -1)∪(8; +∞)
ОДЗ: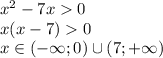
ответ(включая ОДЗ):