Решите неравенство: корень 4-ой степени из x + 1 > 30/x
Другие вопросы по теме Алгебра
Популярные вопросы
- 4. какая пара слов не является словосочетанием: A первый снег пошел быстро...
2 - ТВОРЧЕСКАЯ РАБОТА Какие цифры нужно вставить в кокошки» так, что числа...
3 - . В каких условиях среды происходит движущий и стабилизирующий отборы....
3 - Человек услышал выстрел через 3 с, находясь на расстоянии 1 км от места...
2 - Презентация на тему «Историю Пифагора»...
1 - ОЧЕНЬ !Не выполняя построения, определи, принадлежит ли графику функции...
2 - Біздің отбасымыз үлкен. Біз ағаш отырғызамыз. Атамыз бен әкемізге көмектесеміз....
2 - Какова роль животных ,обитающих в почве ,в повышении её плодородия?...
1 - Задание 3 ( ). В настоящий момент самым скоростным считается лифт в 530-метровом...
3 - қазақ тили 6 сынып 8 тапсырма...
1
ОДЗ:
{х+1 ≥0⇒х≥-1
{x≠0
При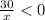 неравенство верно при любом х из ОДЗ
неравенство верно при любом х из ОДЗ
x∈[-1;0) - решение неравенства
При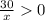 , т.е при x>0 возводим обе части неравенства в четвертую степень:
, т.е при x>0 возводим обе части неравенства в четвертую степень:
Решаем неравенство графически:
См. рис.
Строим графики y=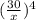 ( красного цвета)
( красного цвета)
при x >0
кривая убывает.
Строим y=x+1 это прямая синего цвета, возрастает на (-∞;+∞)
Кривая и прямая пересекаются в одной точке, это х=15
Поэтому неравенство верно при x > 15
О т в е т. [-1;0) U (15;+∞)
ответ и Объяснение:
в приложении