Решите неравенство
корень(2+x-x²) > -1


не могу понять: имеет ли смысл решения неравенства после нахождения одз выражения под корнем? ведь значение квадратного корня из числа по определению больше -1

Если справа - 1 < 0 , то достаточно решить :

          +                         -                           +

__________[-1]___________[2]____________

                     ///////////////////////////

ответ : [- 1 ; 2]

Так как квадр. корень может принимать неотрицательные значения, то есть    ,то тем более 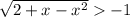    для всех значений переменной "х" из области допустимых значений (ОДЗ).

Поэтому решением неравенства будут те значения переменной "х", которые входят в ОДЗ.

ответ: