1. Алгебра
  2. Решите неравенство и укажите,

Решите неравенство и укажите, сколько натуральных чисел является его решениями: а). log1/5 (2-x)> =log1/5 (2x+4) б). log3 (x2-6x+8)=< 1

avagimyan2002 avagimyan2002    2   17.03.2019 22:00    1

Ответы
egorsinitsyn9Egor egorsinitsyn9Egor  25.05.2020 21:29

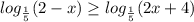
Alog_{\frac{1}{5}}(2-x)\geq log_{\frac{1}{5} }(2x+4)

 

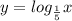  Функция y=log_{\frac{1}{5}}x   - убывающая

  \begin{cases} 2-x\leq2x+4\\2-x0\\2x+40 \end{cases}

  \begin{cases} 2x+x\geq2-4\\x<2\\2x-4 \end{cases}

  \begin{cases} 3x\geq-2\\x<2\\x-2 \end{cases}

  \begin{cases} x\geq\-\frac{2}{3}\\x<2\\x-1 \end{cases}

 

  [-\frac{2}{3};2) В этом промежутке только одно натуральное число равное 1.

  ответ: одно натуральное число

 

B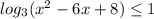log_{3}(x^{2}-6x+8)\leq1

log_{3}(x^{2}-6x+8)\leq log_{3}3

 

функция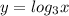 y=log_{3}x возрастающая

 

\begin{cases} x^{2}-6x+8\leq3\\x^{2}-6x+80\ \end{cases}

x^{2}-6x+5\leq0

D=16

x_{1}=5, x_{2}=1

(x-5)(x-1)\leq0

[1;5]

 

 

 

x^{2}-6x+80

D=4

x_{1}=2, x_{2}=4

(x-2)(x-4)0

(-\infty;2)\cup (4;+\infty) -область определения функции

 

 [1;2)\cup (4;5]

 

Здесь два натуральных числа 1 и 5

 

ответ: два натуральных числа

 

 

 

 

 

 

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Max82828 Max82828  16.08.2019 18:30
Выражение 2.5y(4у-(2y-8) и найдите его значение при y= -6...
ДвоечникТочно ДвоечникТочно  16.08.2019 18:30
Решите уравнение корень из x-3=2x-7...
karinkuus karinkuus  16.08.2019 18:30
Уравнение 3х + 6 = 3( х + 2) имеет: а) один корень; б) имеет много корней; в) не имеет корней; г) другой ответ....
Vika7550 Vika7550  16.08.2019 18:30
Функция задана формулой f(x) = - 4x3 + 10. найдите f(2)....
alisaislamova2 alisaislamova2  12.05.2019 12:23
Y=2х 6х+3у=12 {х+у=6 5х-2у=9 {4х+2у=0 5х+2у=0 решите систему уравнений методом сложения...
Розетта99 Розетта99  12.05.2019 12:23
Решить построить неориентированный граф 6 вершин, 9 ребер. найти матрицу смежности инцидентностй, степень вершин путь, цикл, маршрут....
timondrob timondrob  12.05.2019 12:23
Решить линейное уравнение х-3y=1 и 2х это линейное уравнение надо...
Echo12 Echo12  12.05.2019 12:23
Решите, ! sqrt(2) sin x + cos^2x = sqrt(2) sin^3x найти корни уравнения на промежутке: [3pi/2; 3pi]...
demoplus1 demoplus1  12.05.2019 12:26
Произведение двух последовательных целых чисел в 2 раза больше квадрата меньшего из них. найдите эти числа., )​...
antonil70 antonil70  12.05.2019 12:27
Решите уравнение а) 36(x-1)^2+12(x-1)+1=0...

Популярные вопросы