Решите неравенство 2х^2-х-15 0

Question

Алгебра: Решите неравенство 2х^2-х-15 0

GHTU · Answer

Неравенство вида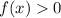 f(x)0 . Найдем нули функции 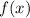f(x) , расставим их на числовой оси и посмотрим на знаки, выберем нужные промежутки

$\displaystyle f(x)=0:~ 2x^2-x-15=0; D=(-1)^2-4\cdot 2\cdot (-15)=121=11^2 \\ x_{1,2}=\frac{1\pm11}{4} \Rightarrow x_1=-\frac{5}{2}; x_2=3$

Имеется 3 промежутка: левый, уходящий в минус бесконечность, средний - между корнями, правый - уходящий в плюс бесконечность.

Возьмем для каждого любое число из промежутка и подставим в функцию:

$f(-5)=2(-5)^2-(-5)-15=2\cdot 25+5-150 ~(+) \\ f(0)=2\cdot0^2-0-150 ~(+)$

Имеем знаки по промежуткам +-+, нам нужен +, так как он в исходном неравенстве, то есть берем

$\boxed{\displaystyle x\in\left(-\infty;-\frac{5}{2}\right) \cup (3;+\infty)}$

Скобки круглые, потому что неравенство строгое и нули функции не включаются.

Решите неравенство 2х^2-х-15 > 0