Решите неравенство
(16^x - 4^x + 1)^2 + 9 * 4^x + 1 < 9 * 16 ^x +36
Другие вопросы по теме Алгебра
Популярные вопросы
- Как сделать защиту футболки по технологии 6 класса...
3 - Реально ли получить из ch2(ok)-ch2(ok) серную к-ту?...
3 - 1)произнеси данные ниже слова поставь в них ударения над ударными...
3 - Какие эпитеты есть в стихотворении весенняя гроза ?...
2 - Какое наибольшее натуральное значение m удовлетворяет неравенству...
3 - Какую летнюю и зимнюю одежду носили в древности народы, населявшие...
2 - Прочитай слоги слияния . в какой группе слов все согласные звуки звучат...
3 - Уреченні хліб випікає пекар зрозуміло,що додатком є слово хліб. у...
2 - 10 предложений про масленицу в любой стране по...
1 - Как решить в столовой за неделю израсходовали 63 кг муки. 4 дня расходовали...
2
Объяснение:
Пусть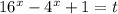
Найдём нули левой части:
Решение неравенства:
Пусть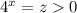
Заметим, что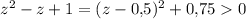 при любых z. Тогда достаточно решить неравенство
при любых z. Тогда достаточно решить неравенство
Найдём нули левой части:
Заметим, что меньший корень отрицателен, а z по замене всегда положительно. Значит, решение неравенства достаточно записать как