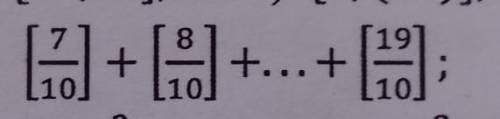
Алгебра: Решите .Найти целую часть числа

Решите .
Найти целую часть числа

Решите .Найти целую часть числа

Ответы

andreiantipov1 07.09.2021 10:48

Здесь от каждой дроби берётся целая часть.

Значит, дроби меньше единицы здесь имеют целую часть, равную нулю:

$$\left[\frac{7}{10}\right]=0;\ \ \ \left[\frac{8}{10}\right]=0;\ \ \ \left[\frac{9}{10}\right]=0$

Все остальные дроби (с числителями от 10 до 19)- каждая имеет целую часть, равную единице: $$\left[\frac{10}{10}\right]=\left[\frac{11}{10}\right]=\left[\frac{12}{10}\right]=\left[\frac{13}{10}\right]=\left[\frac{14}{10}\right]=\left[\frac{15}{10}\right]=\left[\frac{16}{10}\right]=\left[\frac{17}{10}\right]=\left[\frac{18}{10}\right]=\left[\frac{19}{10}\right]=1$ Всего таких дробей 10 штук, что даст общую сумму всего примера, равную:

1 * 10 = 10

Или вот, полностью весь пример: $$\left[\frac{7}{10}\right]+\left[\frac{8}{10}\right]+\left[\frac{9}{10}\right]+\left[\frac{10}{10}\right]+\left[\frac{11}{10}\right]+\left[\frac{12}{10}\right]+\left[\frac{13}{10}\right]+\left[\frac{14}{10}\right]+\left[\frac{15}{10}\right]+\left[\frac{16}{10}\right]+\left[\frac{17}{10}\right]+\left[\frac{18}{10}\right]+\left[\frac{19}{10}\right]=$

$=0+0+0+1+1+1+1+1+1+1+1+1+1=0*3+1*10=10

ответ: 10

P.S.

Целая часть находится делением нацело на 10

Например:

7 : 10 = 0 целых (и 7 в остатке)

10 : 10 = 1 целая (и 0 в остатке)

19 : 10 = 1 целая (и 9 в остатке)

Если бы был знаменатель посложнее, чем 10, то можно было бы делить уголком например. Ну, или на калькуляторе всегда можно поделить и увидеть целую часть дроби.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра