Решите методом интервалов неравенство
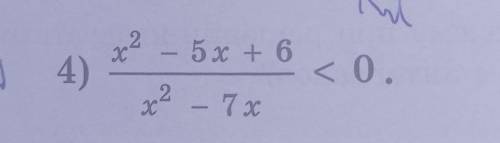
Другие вопросы по теме Алгебра
Популярные вопросы
- Хто були першими лауреатами літературної шевченківської премії...
3 - Придумать и составить сочинение по мой дача my country house...
3 - Запишите три формы следующих глаголов: sanieren, haben, beruhen,...
1 - Отзыв к рассказу белый клык-джек лондон...
3 - Выбери три существительных с каждым из них составь предложения...
2 - Образование обломова .его отношение к учебе науке. отношение...
3 - Сообщение на тему особенности промышленного переворота в енисейской...
1 - Матросы- это точно словарное слово?...
3 - Вычислить массы одного атома гелия и аргона...
2 - Вспомни народную сказку теремок. запиши 4 предложения с прямой...
1
Объяснение:
разложим на множители числитель и знаменатель
x²-5x+6=x²-2x-3x+6=x(x-2)-3(x-2)=(x-2)(x-3)
x²-7x=x(x-7)
(x²-5x+6)/(x²-7x)<0
(x-2)(x-3)/(x(x-7))<0
корни числителя и знаменателя 0; 2;3;7 нанесем их на числовую ось и определим знак выражения (x-2)(x-3)/(x(x-7)) на каждом интервале
для этого будем брать любое число из каждого интервала и подставлять в выражение (x-2)(x-3)/(x(x-7))
x=10 (x-2)(x-3)/(x(x-7))= (10-2)(10-3)/(10(10-7))=(+)(+)/(+)(+)=(+) знак+
x=5 (x-2)(x-3)/(x(x-7))= (5-2)(5-3)/(5(5-7))=(+)(+)/(+)(-)=(-) знак-
x=2,5 (x-2)(x-3)/(x(x-7))= (2.5-2)(2.5-3)/(2.5(2.5-7))=(+)(-)/(+)(-)=(+) знак+
x=1 (x-2)(x-3)/(x(x-7))= (1-2)(1-3)/(1(1-7))=(-)(-)/(+)(-)=(-) знак-
x=-1 (x-2)(x-3)/(x(x-7))= (-1-2)(-1-3)/(-1(-1-7))=(-)(-)/(-)(-)=(+) знак+
0237>
+ - + - +
так как знак неравенства меньше выбираем интервалы со знаком -
х∈(0;2)∪(3;-7)