Решите логарифмическое неравенство
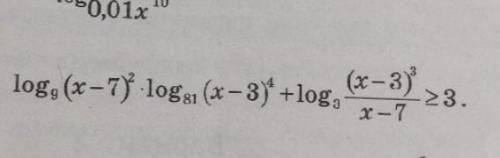
Другие вопросы по теме Алгебра
Популярные вопросы
- Представьте себя подданным Франкского королевства середины VI в. Правитель отправляет...
2 - 1)Установіть відповідність між цифроними позначениями спадкових хвороб (1-4)...
3 - Длина стороны правильного шестиугольника равна 30,72 см. Найди радиус окружности...
3 - Запишите систематику 2 животных типо: кошка царство животных класс кошачьих и...
2 - Напишіть есе на тему Весна використовуючи звертаня...
2 - На рисунку точка О - центр кола, АС — дотична до кола, кцт АВС - 29°. Знайдіть...
3 - Які амінокислоти проявляють властивості а) лише кислоти б) лише основ в) кислото-основні...
3 - У шкільну бібліотеку у понеділок завезли 48% всіх підручників для 5 класів, а...
1 - Почему растения не могут жить без кислорода?...
3 - для функции у=х² найдите значение у ,которое отвечает х= -3 ;4...
2
Объяснение:
ОДЗ:
-∞__+__3__-__7__+__+∞
x∈(-∞;3)U(7;+∞).
1.
1.
2.
ответ: x∈(-∞;3)U[7¹/₂₇;+∞).