Решите иррациональные уравнения 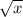 =4
=4
x-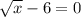
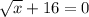
Другие вопросы по теме Алгебра
Популярные вопросы
- Сколько грамм соли в одной тонне воды чёрного моря(18 промиль), во сколько...
1 - Написать сочинение по по произведению жураулины крык по теме: мой любимы...
2 - Выберите одно из предложенных ниже высказываний, раскройте его смысл,...
3 - Решите неравенство 3x²+12x: x²+10х+25 =0...
1 - 6речень з головними членами речення...
3 - Вычислите : а) (2-3i) - (1/3 + 2/5i) b) (5-2i)(1/3 - 7/2i) c) 2-3i/7+i...
1 - Какой образ жизни вели германцы, норманны, славяне, арабы в средних...
3 - Как решить уравнение 4 целых 1/5 + х = 8 целых 3/10...
2 - Написать сообщение на тему культура ивановского края в древности...
3 - Маша и миша массами 30 и 40 кг качаются на однородной доске длиной 5...
2
Объяснение:
Корень t₁ не имеет смысла.