Решите иррациональное уравнение
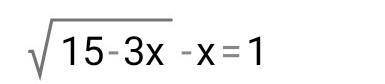
Другие вопросы по теме Алгебра
Популярные вопросы
- Число десятков двузначного числа на 4 меньше его единиц . Произведение двузначного...
1 - Про числа x и у известно,что x - у 0 ...
3 - Поїзд масою 5*10^5 кг рухається зі швидкістю 10 м/с потім почав гальмувати і зупинився...
3 - Тема: Свойства и графики тригонометрических функций Принадлежит графику функции...
3 - с историей буду благодарен)...
3 - Знайдіть координати вектора АО, де точка О - початок координат, А (1; -3; 2) *...
2 - Какой объем воздуха затрачивается на сгорание 10,6 г этилбензола, содержащего...
3 - БУДЬ-ЛАСКА ДО ТЬ твір-мініатюра на 7-10 речень Моє ставлення до вчинку головної...
1 - Допожіть з вправою,будьласка!...
2 - Енергія фотона дорівнює кінетичній енергії електорона що має початкову швидкість...
2
√(15 - 3x) - x = 1
• Перенесём переменную икс вправо, при этом изменив знак:
√(15 - 3x) = 1 + x
• Возведём обе части в квадрат, но при этом напишем область определения:
[ √(15 - 3x) ≥ 0
[ 1 + x ≥ 0
Решив систему, получаем:
[ x ≤ 5
[ x ≥ -1
D ( ƒ ) = [ -1 ; 5 ]
• После возведения в квадрат, мы получили уравнение следующего типа:
15 - 3x = (1 + x)²
• Перенесём обе части уравнения влево, а после упростим:
15 - 3x - (1 + x)² = 0
15 - 3x - 1 - 2x - x² = 0
-x² - 5x + 14 = 0 / • (-1)
x² + 5x - 14 = 0
По теореме, обратной теореме Виета получаем следующие корни:
x₁ = -7 и x₂ = 2
• Следуя из области определения, получаем, что x₁ = -7 - не подходит по условию, ⇒
ответ: x = 2