Решите хотя бы 3 1. выражение: $a)\frac{ \tan^{2} \alpha}{1 \ + \ tan^{2} \alpha } = \\ \\ b)\tan^{2} \alpha - 1 + \frac{1}{\cos ^{2} \alpha } = \\$ 2. известно,что: $\sin\alpha = - \frac{3}{5} \: \: \ \: \: \pi < \alpha < \frac{3}{2} \pi$ найдите: cos a , tg a , ctg a.3. решите уравнения: $a) (\frac{1}{5} )^{ - 2x} = 25 \\ \\ b) log_{3}(3 - 2x) = 2 \\ \\ c) \sin(2x - \frac{\pi}{3} ) = 1 \\ \\ d) \cos^{2}x - 5 \cos \: x + 4 = 0$ 4. 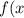найти производную функцию $f(x) = 3 {x}^{2} - \sqrt{x} + {x}^{3 } \\ \\ f(x) = \frac{2 {x}^{2} - 1}{x} \\ \\ f(x) = 2 \cos \: x - 3 \cot \: x$ 5. написать уравнение прямой, проходящей через две точки: a(-3; 7) b(1; -9)

Ответы

Ibrolya 07.07.2020 08:22

в приложении

Объяснение:

$Решите хотя бы 3 1. выражение: [tex] a)\frac{ \tan^{2} \alpha}{1 \ + \ tan^{2} \alpha } = \\ \\ b)\t$
$Решите хотя бы 3 1. выражение: [tex] a)\frac{ \tan^{2} \alpha}{1 \ + \ tan^{2} \alpha } = \\ \\ b)\t$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

anaastasiya04 21.04.2019 21:23

Постройте график линейной функции у = -х + 2. с графика найдите: а) значение у, если х = 2; б) значение х, если у =5; в) значения переменной х, при которых значения функции...

ЗоНя3 21.04.2019 21:20

Выражение 5√3 + √75 − √300. а)19√3; б) − √3; в) − 1; г) √3....

caramelka05 21.04.2019 21:20

При каких значенияx d выражение имеет смысл? [tex] \sqrt{d - 12.5} [/tex]...

ШиноаХиираги 21.04.2019 21:19

Что то не могу понять как решается это , может кто знает?...

pavellolpanov 21.04.2019 21:18

Постройте график функции y=kx+6 если известно сто он прохолит через точку а (2,3)...

Noob335 21.04.2019 21:18

20 с системой ! решить сложения: а) x-3y=4 б) 22x+3y=0 5x+3y=-1 7x-2y=-25...

dddddkkke 21.04.2019 23:04

Объясните, как производная x+c+(1/x)*(1/b) равна одному и почему? ...

Бота20081 21.04.2019 22:54

Квадрат разделен на 6 маленьких квадратов и 5 равных прямоугольника найдите площадь прямоугольника если площадь маленького квадрата равна 42 квадратных сантиметра...

Zhuldyz2005 21.04.2019 22:53

[tex]4\cot{x}-1=2\sin{(2x)}*(3\sin^2{x}+2\cos{(2x)})[/tex] решите тригонометрическое уравнение с полным оформлением, желательно методом разложения на множители....

Sabinakerimli 13.09.2019 19:30

Надо разложить на множители 3)4х-4у+сх-су...

Популярные вопросы