Решите эти примеры (мне нужно решение+ответ, а не просто ответ)
даю за это

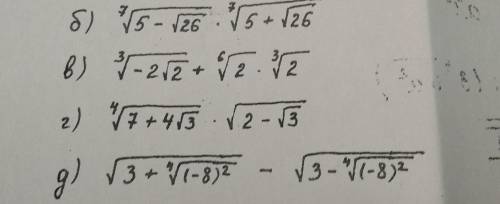
Решите эти примеры (мне нужно решение+ответ, а не просто ответ) даю за это

Ответы

hcunvakjb 08.11.2021 09:10

Объяснение:

б) можно загнать под общий корень

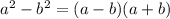твой пример $=\sqrt[7]{(5-\sqrt{26})(5+\sqrt{26}) }=$ по формуле сокращенного умножения a^2-b^2=(a-b)(a+b) = $\sqrt[7]{5^2-\sqrt{26}^2} =\sqrt[7]{25-26} =\sqrt[7]{-1} =$ так как корень нечетный можно выводить из под корня отрицательное число =

= $\sqrt[7]{-1} =-1$

в) по правилу $\sqrt[a]{b^n}=b^{\frac{n}{a} }$

$\sqrt[3]{-2\sqrt{2} }+\sqrt[6]{2} *\sqrt[3]{2}=\sqrt[3]{-2\sqrt{2} }+\sqrt[6]{2} *2^{\frac{1}{3} }=\sqrt[3]{-2\sqrt{2} }+\sqrt[6]{2} *2^{\frac{2}{6} }=\sqrt[3]{-2\sqrt{2} }+\sqrt[6]{2} *\sqrt[6]{4}$

коротко если говорить я сделал знаменатель равным 6-ти, чтобы объединить корни

$\sqrt[3]{-2\sqrt{2} }+\sqrt[6]{2} *\sqrt[6]{4}=\sqrt[3]{-2\sqrt{2} }+\sqrt[6]{2*4}=\sqrt[3]{-2\sqrt{2} }+\sqrt[6]{8}$

вынесем минус

$-\sqrt[3]{2\sqrt{2} }+\sqrt[6]{8}= -\sqrt[3]{2\sqrt{2} }+\sqrt[3]{2\sqrt{2} }=0$

почему?

$\sqrt[6]{8}=\sqrt[6]{2*4}=\sqrt[6]{2*2^2}=\sqrt[6]{\sqrt{2}^2*2^2 } =\sqrt{2}^{\frac{2}{6} }*2^{\frac{2}{6} }= \sqrt{2}^{\frac{1}{3} }*2^{\frac{1}{3} }=\sqrt[3]{2\sqrt{2} }$

$-a+a=0\\a=\sqrt[n]{2\sqrt{3} }$

еще 2 примера

ну ладно

$\sqrt[4]{7+4\sqrt{3} } *\sqrt{2-\sqrt{3} }$

чтобы сделать под общий корень, нужно чтобы степень корней была одинакова

$=\sqrt[4]{(7+4\sqrt{3})((2-\sqrt{3})^2) } =$

формула сокращенного умножения

$\sqrt[4]{(7+4\sqrt{3})(4-4\sqrt{3}+3) }=\sqrt[4]{(7+4\sqrt{3})(7-4\sqrt{3})} =\sqrt[4]{49-48} =\sqrt[4]{1} =1$

тут всё знакомо с предыдущих

ну кроме того что $\sqrt{x} =\sqrt[2]{x}$ = $\sqrt[4]{x^2}$ = $x^{\frac{2}{4} }=x^{\frac{1}{2} }$

d) $\sqrt{3+\sqrt[4]{(-8)^2}} -\sqrt{3-\sqrt[4]{(-8)^2}}=\sqrt{3+\sqrt[4]{64}}-\sqrt{3-\sqrt[4]{64}}=\sqrt{3+\sqrt[4]{2^6}}-\sqrt{3-\sqrt[4]{2^6}}=\sqrt{3+2\sqrt{2} }-\sqrt{3-2\sqrt{2} }$