Решите если возможно 8-10. вас
Другие вопросы по теме Алгебра
Популярные вопросы
- Выполните действия: а) -13,6 · (-7,2 + 313,2 : 8,7); б) -16,3 · (-8,3...
2 - У папороті корені та пагони мають особини...
1 - Гидрореактивный катер всасывает и выбрасывает ежесекундно V_0 = 0.5...
2 - В первом классе 31 ученика, во третьем - на 4 ученика меньше, чем в...
2 - Сравнительная характеристика русских земель в Великом княжестве Литовском...
1 - Сравнить физико-географическую карту Восточной Сибири и карту политико...
1 - Почему было арестовано Мигеля де Сервантеса?...
2 - Визначте молекулярну формулу аміну ,в якому масова частка карбону становить...
1 - Как вы думаете почему случай с загнанной лошадью получил такой живой...
1 - Из каждой пары выберите словосочетание с переносным значением. Золотая...
1
Объяснение:
8.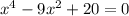
Замена: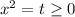
Обратная замена: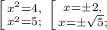
9.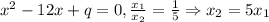
По теореме Виета: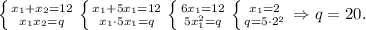
Второй корень: x₂= 5 · 2 = 10.
10.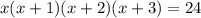
Отдельно перемножим первый и четвертый, второй и третий множители:
Замена: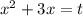
Обратная замена:
Итого: x₁ =-4, x₂ = 1.