Решите два логарифмических уравнения.

Другие вопросы по теме Алгебра
Популярные вопросы
- Какова роль междоузлий в жизни растений?...
1 - Заполните пропуски: 2-3*=; - это пропуски,решать в столбик....
3 - Составте словарный диктант из 10 слов по теме причастие...
1 - На одном недавно состоявшемся придворном турнире по притворной было предложено...
3 - Найти производную заданной функции y=(x+1)^2tg8x...
3 - Хто зайвий: зяблик,повзик,зозуля, ластивка. чому?...
3 - Содного участка собрали 62 ящика помидор, а совторого 57 таких же ящиков помидор....
1 - 1)какой вид имеет треугольник, в котором больший угол меньше суммы двух других...
2 - Составьте уравнения реакций,при которых можно осуществить следующие превращения:...
2 - Радианная мера круга: 135,270,120,105,75,100,140 формулу я знаю,с простыми...
1
1)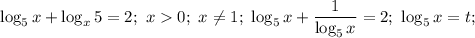
Проверка: 1+1=2 - верно.
ответ: 5
2)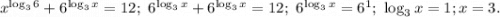
ответ: 3
Мы воспользовались формулой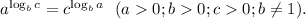
Ее можно доказать, прологарифмировав левую и правую части по основанию b.