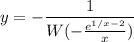(решите дифференциальные уравнения с разделяющими перемеными и найти их частные (x×y^2+y^2)dx +(x^2-x^2×y)dy=0 y=1, x=1
Другие вопросы по теме Алгебра
Популярные вопросы
- Алибек пен атасы кайда барады....
2 - 2. Измени слова. Игра «Один – много».ковш-Малыш —шалаш -Каландаш...
3 - Не или ни? Докажи своё мнение. Пример: «Н_ раз он о сказанном»....
2 - Есептік сан есім 5 мысал Реттік сан есім 5 мысалДара сан есім...
3 - Чему равна масса химическщого элемента?...
1 - Найдите дискриминант 7x²+6x+1=0...
2 - 1. Баскетбол: Принимать мяч надёжнее … . (Назовите два пропущенных...
2 - Найти импульс фотона, излученного при переходе электрона с 5...
3 - решить тригонометрическое уравниние tg⁴-4tg²x+3=0...
3 - Task 4. Write the sentences in Direct speech.1. She said she...
3
Найдём частное решение:
Откуда имеем: