Решите дифференциальное уравнение
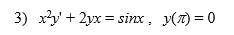
Другие вопросы по теме Алгебра
Популярные вопросы
- Побудувати ланцюжок iнтервалiв вiд ноти МI-БЕМОЛЬ(вгору в.2-...
2 - На клетчатой бумаге с размером клетки 1×1 изображен треугольник....
1 - 14. 35 Составьте ситуации со следующими словами и словосочетаниями...
2 - До ть будь ласка 2 та 3 завдання...
1 - 6. Выберите из перечня утверждений те, которые раскрывают суть...
3 - Как называется художественно-выразительное использованию словосочетаниях...
2 - Сторони трикутника ABC: 22 см, 20см, 14 см. з вершини найменшег...
1 - Определите синтаксическую роль личного местоимения 2 лица единственного...
2 - перевести на английский язык ...
1 - Из 20 учащихся класса каждый изучает хотя бы один иностранный...
2
левую часть уравнения можно свернуть
тогда